“Physics is too difficult for physicists.” – David Hilbert
Operator theory is one of the foundations of Quantum Mechanics and it’s one of those mathematical areas that stores the craziest things that can possibly happen in what we call reality. And the theorem we will talk about today, is a way of shedding light into the dark universe of Hilbert spaces. This is the most powerful theorem in Operator Theory, called the Spectral Theorem.
Check out the free PDF right here:
We’d like to keep our videos free of interruptions and sponsors, so that the sole focus is the subject at hand. But in order to do that we need your help.
If you find value in our videos and would like to support our work further, and get very useful info that is unavailable anywhere else, consider purchasing this Full PDF on the Spectral Theorem
This PDF will give you a clear introduction to the spectral theorem through the concrete example of the Dirichlet Laplacian operator on the Hilbert space. We will look at definitions of self-adjoint and normal operators, verify the self-adjointness of the Laplacian via integration by parts, and use the spectral theorem to explicitly compute its spectral decomposition in terms of eigenvalues and normalized eigenfunctions. The PDF includes 7 exercises with detailed solutions, as well as an appendix. Thank you for supporting our work, it means a lot to us!
In any case, if you don’t have the means, we always have our free videos. Thanks again!
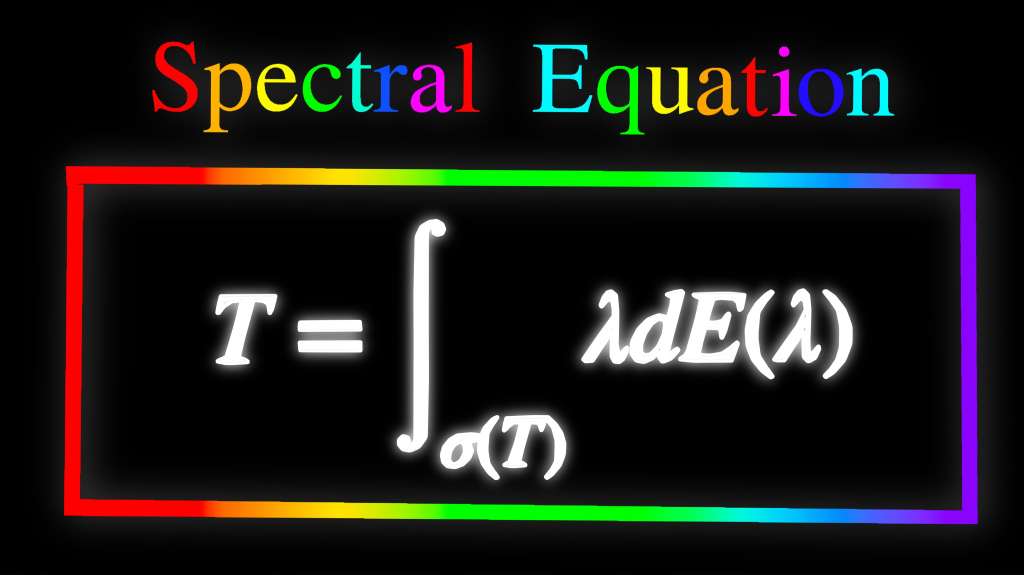
Leave a comment