DiBeos

What is pure math, really? Even though some people might say it’s the language the universe is written in, at its very core, pure math studies mathematical concepts which are independent of any application.

Applied math, for example, is driven by solving practical problems in immediate fields like physics and engineering. But pure math is by pure curiosity. So, sometimes you can’t really know if what you’re studying will ever be useful practically speaking.

So then, we’re forced to clear up: what kinds of things does pure math study?

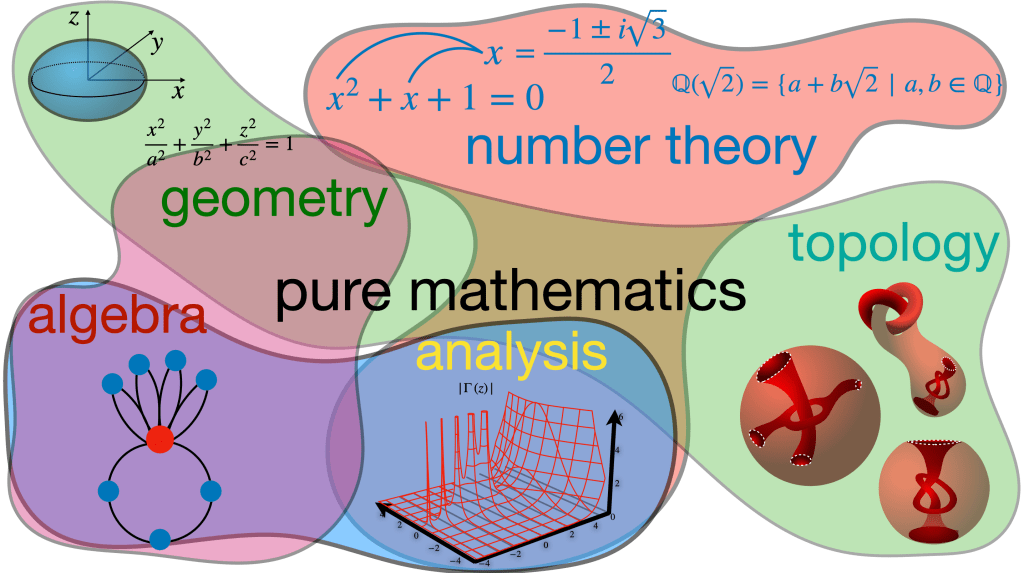
Well, first of all, the foundations of pure mathematics can be grouped into major areas like algebra, geometry, number theory, analysis, and topology. Each of these studies all kinds of different concepts. But here’s the thing: over time, the lines between these areas have blurred, and mathematicians have to get ideas from multiple fields to solve problems. 

The amount of things you can study in math is pretty huge. Some mathematicians focus on logic and set theory, which is the absolute base of mathematical thought that focuses on how any subject can be built up from a small collection of axioms. Other mathematicians go for abstract algebra, with infinite-dimensional Lie algebras, universal algebra, or some aspects of something called homological algebra. Then there’s algebraic topology, which studies properties of spaces that remain unchanged under continuous deformations, and it uses very abstract tools like homotopy and cohomology. We can go on forever with this. The point is that a lot of pure math has concepts which are, at least currently, unapplicable. 

A very interesting field I’d like to point out, sometimes considered to be the purest of the pure math fields, is number theory. Number theory is all about the properties of numbers, especially integers. Concepts like primes, congruences, Diophantine equations, and so on, interest mathematicians not because they have immediate applications, but because they often have beautiful, deep, and sometimes unsolvable problems to explore. 

Although ironically, despite number theory being considered one of the lesser applied fields, it’s actually hugely important in modern cryptography, which we pretty much can’t get by in the modern world. 

Anyway, not every branch of pure math finds applications, and that’s okay. Pure math often starts with no usefulness at all; it’s developed just out of intellectual curiosity. Mathematicians ask themselves, “What if we define this structure?” or “What properties would follow if we accept this new axiom?” And from that, entire fields can emerge. These new fields sometimes remain nothing but theoretical curiosities for centuries before anyone finds a real-world use for them, if they ever do.

So that raises a big philosophical question: Why should we do it at all? Sure, we can’t really predict what might be useful in the future, but we have some ideas of what appears to be pretty useless for the real world. Like, what will ever be the point of proving that the Boy’s surface is homeomorphically equivalent to the real projective plane? (Which is something I studied in my Master’s, by the way). Or, what’s the point of finding out how many primes there are? Or, why would we ever need to prove the Goldbach Conjecture? Which says that every even integer greater than 2 is the sum of two primes. I mean, why would humanity ever need that?

Well the thing is, mathematicians don’t always agree on what is the purpose of pure math. For some, it’s about truth, logical truth that is independent of the physical world. For others it’s about the elegance of a proof, so in other words beauty. It’s always incredible to know exactly how and why a complex idea just fits into place. There’s even debate about what it means for something to be “true” in mathematics. Because if we’re honest, mathematical truths depend on the axioms we initially started with. Change the rules, and you change the universe you’re working in.

So, can you even say that pure math is something real? That depends on your philosophy of mathematics. Are mathematical objects discovered or are they invented? so can it be possible that they are just a creation of the human mind? Whatever your opinion is on this, we can’t deny that pure math gives us the tools to explore those objects, wherever it is that they come from.

This is not to mention that over time, even the most abstract mathematics can find its way into the world. Complex numbers, non-Euclidean geometry, group theory: all of these at some point were seen as pointless. But today, you can’t get by without them in fields like physics, cryptography, signal processing, and so on.

Still, let’s stress that the value of pure math isn’t measured by how useful it is in the real world. If we were to narrow it down, it’s probably fair to say that the heart of pure math is in the fact that it studies truth itself, which is something more fundamental than anything. 

Next time you hear someone say that math is only useful for engineers and bankers, and I mean clearly this person hasn’t studied math, but anyway, remind them that pure math is the source of pretty much all ideas through logic and structure.

Even if it won’t lead anywhere practical, math will definitely lead you somewhere beautiful.